INTRO

Hola usuarios de mi blog, este esta dedicado a algunos conceptos básicos y utilidades para estudiantes de primaria ,secundaria y hasta universitarios.

DEFINICIONES BÁSICAS

ALUMNO: Es la persona matriculada en cualquier grado de los diversos niveles, servicios, modalidades y programas del Sistema Educativo.
AULA: Área destinada a impartir clases en un centro de enseñanza.

DOCENTE: Persona en el proceso de enseñanza aprendizaje, desempeñando funciones pedagógicas impartiendo conocimientos y orientando a los alumnos.

ENTIDAD: Se refiere a un estado de la República Mexicana, en nuestro caso Jalisco

ESCUELA: Conjunto organizado de recursos humanos y físicos que funcionan bajo una autoridad de un director o responsable, dedicado a impartir educación a estudiantes de un mismo nivel educativo y con un turno y horario determinado.

GRADO: Se refiere a cada una de las etapas en que se divide un nivel educativo. A cada grado corresponde un conjunto de conocimientos.

GRUPO: Es un conjunto de alumnos que estudian, en una misma aula y en un mismo horario, las materias o los cursos establecidos por un plan de estudios correspondiente a un grado escolar.

MATRÍCULA: Es el conjunto de personas anotadas en una lista o registro para un fín determinado (La Educación).

MODALIDAD: Es la primer gran división del sistema educativo nacional que indica de que manera se imparte la educación; para ello se divide en dos partes: modalidad escolarizada y modalidad no escolarizada.

NIVEL EDUCATIVO: Cada una de las etapas que forman la educación de un individuo tomando como base un promedio de edad determinada. El cual al finalizar se le otorga un certificado de acreditación del nivel en cuestión.

PROGRAMA: Son los diversos planes escolares que ofrecen los niveles educativos.
SERVICIO: Es un conocimiento que se caracteriza por no ser propedéutico y estar fuera de los niveles educativos, en algunos casos tiene la finalidad de preparar al educando para que ingrese a la fuerza de trabajo.

SOSTENIMIENTO: Es el organismo que proporciona los recursos para el financiamiento del centro de trabajo.

DEFINICIONES DE INDICADORES

INDICADORES EDUCATIVOS: Instrumentos que nos permiten medir y conocer la tendencia y las desviaciones de las acciones educativas, con respecto a una meta o unidad de medida esperada o establecida; así como plantear previsiones sobre la evolución futura de los fenómenos educativos.
ABSORCIÓN: Es el indicador que permite conocer el porcentaje de egresados de un nivel educativo, que logran ingresar al nivel educativo inmediato superior. 

COBERTURA: Es la proporción de alumnos atendidos en un nivel educativo con respecto a la demanda. 

ABANDONO ESCOLAR INTRACURRICULAR: Es el porcentaje de alumnos que abandonan el sistema educativo durante el ciclo escolar.

ABANDONO ESCOLAR (TOTAL): Es el porcentaje de alumnos que abandonan el sistema educativo durante el ciclo escolar y/o no se reincorporan al proximo ciclo escolar.

EFICIENCIA TERMINAL: La Eficiencia Terminal permite conocer el porcentaje de alumnos que terminan un Nivel Educativo de manera regular (dentro del tiempo establecido) 

REPROBACIÓN: Es el indicador que permite conocer el porcentaje de alumnos, que al no haber acreditado las asignaturas o créditos escolares mínimos establecidos por las instancias educativas, no serán sujetos a promoción al siguiente grado o nivel educativo y que a partir de secundaria los alumnos que no aprueben una materia seran considerados como reprobados aun cuando puedan pasar al nivel o grado siguiente. 

Deslizamiento

Daños causados por deslizamientos de lodo en el centro de Puerto Ricodespués del huracán Georges.

Un deslizamiento es un tipo de corrimiento o movimiento de masa de tierra, provocado por la inestabilidad de un talud.

Se produce cuando una gran masa de terreno se convierte en zona inestable y desliza con respecto a una zona estable, a través de una superficie o franja de terreno pequeño espesor. Los deslizamientos se producen cuando en la franja se alcanza la tensión tangencial máxima en todos sus puntos.

Estos tipos de inestabilidades son evitables por medios técnicos. Sin embargo, el resto de tipos de corrimientos (flujo de arcilla, licuefaccióny reptación) resultan más difíciles de evitar.

Un ejemplo de deslizamiento en masa se produjo en la Presa de Vajont, en el noreste de Italia en 1963 y ocasionó la muerte de unas 2000 personas, al caer en la presa centenares de millones de m³ de tierra, árboles y rocas, causando una ola gigantesca que arrasó varias poblaciones de la cuenca, en especial, a Longarone.

Los deslizamientos también son causados por las lluvias que humedecen y aguadan el suelo, también debido a un pequeño sismo en las placas tectonicas.

SIMETRÍA CENTRAL

VIDEO 1

VIDEO 2

SIMETRÍA AXIAL

Una simetría axial de eje e es una transformación, por tanto a todo punto P del plano le corresponde otro punto P' también del plano, de manera que el eje e sea la mediatriz del segmento AA'.

Las simetrías axiales son isometrías porque conservan las distancias entre los puntos y sus homólogos.

Coordenadas de puntos mediante simetrías axiales

1 Coordenadas de un punto simétrico al eje de ordenadas

Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de ordenadas tienen sus abscisas opuestas y sus ordenadas iguales.

P(x, y)  P(-x, y)

x = -x' y = y'

2 Coordenadas de un punto simétrico al eje de abscisas

Dos puntos A(x, y) y A'(x', y') simétricos respecto del eje de abscisas tienen sus abscisas iguales y sus ordenadas opuestas.

P(x, y)  P(x, -y)

x = x' y = -y'

Composición de simetrías axiales

1 Simetría de ejes paralelos

La composición de dos simetrías ejes paralelos e y e' es una traslación, cuyo vector tiene:

La longitud del vector es el doble de la distancia entre los ejes.

La dirección del vector es perpendicular a los ejes.

El sentido es el que va de e a e'.

2 Simetría de ejes perpendiculares

La composición de dos simetrías de ejes perpendiculares e y e' es una simetría central respecto del punto de corte de los dos ejes de simetría.

3 Eje de simetría

ROTACION

Rotación es el movimiento de cambio de orientación de un cuerpo o un sistema de referencia de forma que una línea (llamada eje de rotación) o un punto permanece fijo.

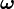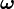La rotación de un cuerpo se representa mediante un operador que afecta a un conjunto de puntos o vectores. El movimiento rotatorio se representa mediante el vector velocidad angular , que es un vector de carácter deslizante y situado sobre el eje de rotación. Cuando el eje pasa por el centro de masa o de gravedad se dice que el cuerpo «gira sobre sí mismo».

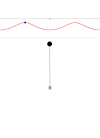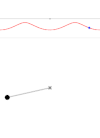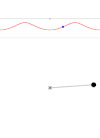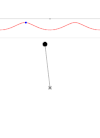
La rotación también puede ser oscilatoria, como en el péndulo (izquierda). Los giros son completos sólo cuando la energía es lo suficientemente alta (derecha). El gráfico superior muestra la trayectoria en el espacio fásico.

En ingeniería mecánica, se llama revolución a una rotación completa de una pieza sobre su eje (como en la unidad de revoluciones por minuto), mientras que en astronomía se usa esta misma palabra para referirse al movimiento orbital de traslación de un cuerpo alrededor de otro (como los planetas alrededor del Sol).

HOMOTECIA

VÍDEO DE EJEMPLO HOMOTECIA

Homotecia

Definición

Se llama homotecia de centro O y razón k (distinto de cero) a la transformación que hace corresponder a un punto A otro A´, alineado con A y O, tal que: OA´=k·OA. Si k>0 se llama homotecia directa y si k<0 se llama homotecia inversa.

Homotecias de centro el origen de coordenadas

En una homotecia de origen el centro de coordenadas se puede ver con facilidad la relación que existe entre las coordenadas de puntos homotéticos. Si se considera A(x,y) y su homotético A´(x´,y´) la relación que hay entre ellos es la siguiente: x´=kx    y´=ky

Teorema de Tales. Semejanza de polígonos

Teorema de Tales

Si se cortan varias rectas paralelas por dos rectas transversales, la razón de dos segmentos cualesquiera de una de ellas es igual a la razón de los correspondientes de la otra. En el ejemplo de la escena Descartes siguiente tres rectas paralelas son cortadas por dos secantesr y s y puede comprobarse en todo momento qué valor alcanzan los segmentos determinados en estas dos rectas y sus cocientes, que son siempre iguales.

Semejanza de triángulos

Dos triángulos son semejantes cuando tienen sus ángulos iguales y sus lados proporcionales; es decir, si los triángulos ABC y A´B´C´ son semejantes se verifica:

A=A´    B=B´    C=C´        AB/A´B´=BC/B´C´=CA/C´A´=razón de semejanza

ESCALAS

La representación de objetos a su tamaño natural no es posible cuando éstos son muy grandes o cuando son muy pequeños. En el primer caso, porque requerirían formatos de dimensiones poco manejables y en el segundo, porque faltaría claridad en la definición de los mismos.
Esta problemática la resuelve la ESCALA, aplicando la ampliación o reducción necesarias en cada caso para que los objetos queden claramente representados en el plano del dibujo.
Se define la ESCALA como la relación entre la dimensión dibujada respecto de su dimensión real, esto es:

E = dibujo / realidad

Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será de reducción en caso contrario.

Basado en el Teorema de Thales se utiliza un sencillo método gráfico para aplicar una 
escala.

   Véase, por ejemplo, el caso para E 3:5

1º) Con origen en un punto O arbitrario se trazan dos rectas r y

s formando un ángulo cualquiera.

2º) Sobre la recta r se sitúa el denominador de la escala

(5 en este caso) y sobre la recta s el numerador

(3 en este caso). Los extremos de dichos segmentos son A y B.

3º) Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.

Efecto del dibujo a escala sobre las magnitudes lineales, el área y volumen

para conocer el efecto que produce el dibujo a escala sobre las magnitudes lineales, se analizará lo que ocurre cuando se amplía un rectángulo de dimensiones a y b hasta obtener un rectángulo de dimensiones ka y kb.

    

Obsérvese la relación que se establece entre el perímetro P del rectángulo original y el perímetro P´ del rectángulo ampliado:

  P = 2a + 2b

y que P´ = 2(ka) + 2(kb)

     Factorizando k, se obtiene:

P´ = k(2a + 2b)

     Sustituyendo P´ = 2a + 2b, se llega a P´ = kP.

     El perímetro P se transformó igual que la base y la altura del rectángulo.

     A continuación se verá si ocurre lo mismo con las áreas.

A = ab A´ = (ka) + (kb) A´ = k2ab A´ = k2(A)

     Si las longitudes se transforman con una escala k, entonces el área se transforma con una escala k2.

     Véase lo que ocurre con la longitud de una circunferencia y con el área de un círculo:

     Supóngase que el radio del círculo se transformó con una escala de k <1.

     Si se comparan las dos medidas de las circunferencias, se tiene que:

     La longitud de la circunferencia se transformó con una escala igual que la de la modificación del radio.

     Para las áreas se tiene:

     Nuevamente se observa que la razón o escala de las áreas es el cuadrado de la escala con la que se transforman las longitudes.

     Resumen:

• Efecto de las medidas angulares. Siempre que dos figuras o dos sólidos estén a escala, existe semejanza entre ellos; debiendo cumplirse la condición de tener sus ángulos homólogos iguales, pues la medida de un ángulo no la determina la longitud de los lados que lo forman, sino laabertura que hay entre dichos lados; además, sus lados homólogos son proporcionales.

• Efecto en las medidas lineales y perímetros. Dos polígonos a escala son semejantes y cumplen, necesariamente, con dos condiciones: tener sus ángulos homólogos iguales y sus lados homólogos proporcionales.

• Efecto de las áreas. La razón de las áreas de dos polígonos semejantes es igual al cuadrado de la escala dada.

• Efecto en los volúmenes. La razón de los volúmenes de dos sólidos semejantes es igual al cubo de la escala dada.

MEDIA PROPORCIONAL

O media geométrica es cada uno de los términos medios de una proporción geométrica continua, o sea, cada uno de los términos medios de una proporción geométrica, cuando son iguales. Así, en la proporción 8:4::4:2 la media proporcional es 4.

TEOREMA

La media proporcional es igual a la raíz cuadrada del producto de los extremos.

Sea la proporción continua 
vamos a demostrar que 

En efecto: ya sabemos por la propiedad fundamental que ac=bb, o sea, ac=b2.

Extrayendo la raíz cuadrada a ambos miembros, tenemos: 

Y simplificando: 
que era lo que queríamos demostrar.

EJEMPLO

En 
tenemos que 
.

Cuarta proporcional es cualquiera de los cuatro términos de una proporción geométrica discreta. Así, en la proporción 8:16::5:10, cualquiera de estos cuatro términos es cuarta proporcional respecto de los otros tres.

EJEMPLO.

Hallar una cuarta proporcional de 20, 1/3 y 2/5.

Se forma una proporción geométrica con estas tres cantidades, poniendo de último extremo x y se despeja el valor de x: 20:1/3::2/5:x.

Despejando x: 

Sustituyendo el valor de x: 20:1/3::2/5:1/150.

Vídeos relacionados

18 Geogebra y Matemáticas. Transformaciones I

19 Geogebra y Matemáticas. Transformaciones II